Объединенный научный журнал,
2003год, № 30, стр. 68-72
К вопросу о модели микромира.
Гипотезы, приложения.
Е.А.Трофимов
к.т.н.
Большинство современных достижений науки и техники так или иначе связано с открытиями в квантовой физике и в первую очередь, с нашими представлениями о строении материи. Однако, еще до сих пор здесь остаются белые пятна. В данной работе сделана попытка подойти к решению ряда проблем, обсудить некоторые вопросы геометрии микромира и построения модели атома, а также некоторые вопросы прикладного характера, вытекающие из теоретических посылок. Работа рассчитана на широкий круг читателей.
Формальное описание представлений человека об окружающем мире началось с геометрии Евклида, который в 3 веке до н.э. в своем сочинении «Начала» подвел итог трехсотлетнему развитию греческой математики и создал прочный фундамент для дальнейших математических исследований. Геометрия, писал Кант, является наукой, определяющей свойства пространства. Другими словами, основания геометрии вытекают из той очевидности, какой представлено само пространство.
Строго говоря, «Начала» Евклида имеют логические недостатки, которые были полностью выяснены в конце 19 века. Тогда же была создана полная аксиоматика современной евклидовой геометрии [1]. Центральным звеном в аксиоматике Евклида является пятый постулат о параллельных прямых. Гаусс писал: « В области математики немного найдется вопросов, о которых писалось бы так много, как о проблеме в началах геометрии при обосновании теории параллельных линий. Мы за две тысячи лет нисколько не ушли в этом вопросе дальше Евклида».
Сейчас уже известно, что «Начала» Евклида не единственная математически мыслимая теория пространства. Почти два столетия назад Н.И. Лобачевский наглядно показал это, приняв аксиому параллельности только за предположение, и заменив ее на противоположное утверждение. Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие ее. Сохранив остальную аксиоматику Евклида, на этой основе Лобачевский логически построил совершенно новую, неевклидову геометрию, где пространство обладает кривизной. И это действительно так. Реальное пространство Вселенной действительно обладает кривизной и его геометрия отличается от Евклидовой.
Поскольку идеальная, воображаемая картина Вселенной, строго говоря, не соответствует реальному положению вещей, попробуем разобраться, не нарушаются ли евклидовы постулаты и для микромира, и если да, то при каких условиях и какую мы получим в этом случае геометрию?
Одним из основных понятий геометрии является точка. Евклид определил ее, как то, что не «имеет частей». Другими словами, точка не должна иметь размера.
Современная математика определяет точку, как совокупность координат. Точка n-мерного пространства определяется множеством отрезков – координат от некоторого гипотетического начала координат. А теперь зададим вопрос: можем ли мы в микромире точно определить длину отрезка, то есть точно определить координаты точки?
В действительности этого сделать нельзя. Существует принцип неопределенности Гайзенберга [2], связывающий погрешность измерения импульса ΔP и координаты ΔX с постоянной Планка h
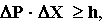
согласно которому точность определения координаты ограничена ΔX . И это значение не может быть равно нулю.
В этом случае, за счет неточности измерения координат, точка будет представлять некоторую размытую область, имеющую размеры.
Если следовать классическому определению, математическая точка не имеет размера. Но, в силу принципа неопределенности, точка для микромира будет представляться, как геометрическое место вероятного нахождения этой точки, в виде размытого пятна. На плоскости можно изобразить точку условно в виде круга диаметром ΔX.
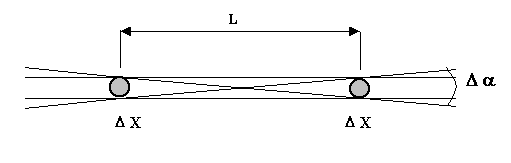
Попробуем провести между двумя такими точками прямую линию.
В этой ситуации мы будем иметь геометрическое место вероятных прямых линий, проведенных между вероятными точками. Все эти прямые линии будут считаться параллельными, поскольку они проведены через две точки. Таким образом, в нашей геометрии нарушается первый постулат Евклида: между двумя точками здесь можно провести бесконечное множество различных параллельных прямых. Причем, при продолжении линий в бесконечность они будут представлять собой расходящийся пучок с углом расхождения этого пучка -Δα, который является своего рода угловой неопределенностью. Угол расхождения Δα (уголовая неопределенность) зависит от расстояния между точками L
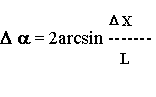
При увеличении расстояния между точками угловая неопределенность Δα стремится к нулю. В этом частном - предельном случае наша геометрия переходит в геометрию Евклида. Когда расстояние между точками становится соизмеримым с размером точки ΔX угловая неопределенность приближается к двум прямым углам
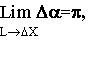
и все прямые линии становятся параллельными друг другу [3]. Естественно, если мы будем рассматривать не плоскую, а пространственную модель, то получим тот же результат.
Таким образом, мы получили очень интересный вывод – в микромире няльзя говорить о направлении, поскольку в этом предельном случае все прямые линии становятся параллельными между собой. Классическое определение направления движения, а значит и классическое определение движения для микромира становится некорректным. Из этого не следует, что в микромире отсутствует движение. Наоборот, с появлением теории относительности и доказательством отсутствия эфира стало понятно, что в природе не существует абсолютного покоя.
Итак, поскольку все прямые линиии в микромире параллельны друг другу, то собственное движение элементарных частиц в микромире должно рассматриваться как однонаправленное, а значит и прямолинейное. Этот вывод очень важен для дальнейших построений.
Проблемы моделирования процессов в микромире возникают в первую очередь из-за двойственной природы элементарных частиц, в частности электрона. Электрон проявляет свойства и частицы и волны. Оба эти качества электрона в равной степени обеспечивают согласие с экспериментом.Уже на заре квантовой физики стало понятно, что у волн-частиц классических линий движения обнаружить нельзя. Например, А.С.Компанеец в своей работе пишет [2] “ ...нет физического определения траектории движения применительно к электронам в атомах. Само понятие траектории, к которому мы так привыкли в повседневном опыте, утрачивает смысл в микромире “. Это довольно близко к нашему выводу, но не затрагивает вопроса об однонаправленности и прямолинейности движения элементарных частиц в микромире.
Здесь может последовать возражение - а как же мы наблюдаем траекторию движения элементарной частицы в ускорителе, причем эта траектория не обязательно прямая линия? Никокого противоречия не возникает, поскольку ускоритель и наблюдаемая траектория уже относится не к микромиру, а к объектам реального мира.
Мы получили некоторую модель пространства, отступив от понятия точки, как ее определил Евклид, причем вполне обоснованно, опираясь на принцип неопределенности Гайзенберга.
Попытки построить модель атома начались с момента открытия электрона. Существовало множество моделей, но наибольшее признание получила планетарная модель атома Резерфорда-Бора.Здесь мы не будем подробно останавливаться на всех аспектах этой модели, отметим только, что она наиболее полно и математически доказуемо объясняет многие явления микромира. Однако и эта модель имеет ряд противоречий, и первое из них связано с двойственной природой электрона. Если электрон – частица, имеет заряд, то при вращении по орбите вокруг ядра атома постоянно меняется его скорость, а значит по законам электродинамики атом должен излучать электромагнитные волны. При этом электрон должен терять энергию и в итоге упасть на ядро. Но этого не происходит – атом не излучает и он стабилен. Если электрон – волна, то почему он имеет массу и можно наблюдать траекторию электрона, вылетевшего из атома, словно это частица? Э.Шредингер, пытаясь соединить эти факты, представлял электрон в виде волнового пакета, «расплывшегося по всему атому». Однако, волновой пакет может рассматриваться (математически обоснованно) как частица только в частном случае, при движении его по прямой линии [4]. Этот факт и повлиял на то, что идея Э.Шредингера не имела дальнейшего развития. Принимая во внимание вывод, который мы получили при построении геометрии микромира, предположение Э.Шредингера становится не так уж и необоснованным и должно, вероятно, иметь развитие.
Очень сложно представить, что электрон, вращаясь по орбите вукруг ядра, двигается прямолинейно, причем одновременно во всех направлениях. Во всяком случае, это следует из наших построений. Физику этого процесса представить так же сложно, как и физику пространства Лобачевского. Все эти проблемы Н.Бор относил за счет того факта, что для описания микромира физики вынуждены пользоваться языком макромира.
Учитывая, что движение в микромире характеризуется однонаправленностью и прямолинейностью, можно объяснить и отсутствие электромагнитного излучения атомов и их стабильность.
Некоторые приложения
Здесь мы остановимся на некоторых вопросах, связанных с внешним резонансным воздействием на атомы (молекулы) и химические реакции. Известно множество видов резонансного воздействия различных видов излучений на вещество. К ним относится, например ядерный гамма-резонанс (эффект Мессбауэра) - поглощение -квантов атомными ядрами в твердом теле, обусловленное ядерными переходами, не сопровождающимися изменением колебательной энергии тела. Еще один вид резонанса - ядерный магнитный резонанс, который характеризуется резким поглощением электромагнитных волн, обусловленным квантовыми переходами атомных ядер между энергетическими состояниями с различными ориентациями спина ядра (наблюдается в диапазоне частот 106 –107 Гц). Эти и другие подобные явления находят широкое применение в исследованиях структуры материи, биологии и др.
Резонансные явления проявляются не только в ядерной физике, но и в обычных химических реакциях. Академик Кузнецов П.Г. в своей работе «Фотоника» [5] отмечает: « ... именно Эйнштейн и был тем человеком, который связал фотоэффект с химической реакцией. Так появилась радиационная теория катализа, ныне уже забытая». Рассматривая механизм катализа химических реакций внешним воздействием, он пишет: «Если резонансный фотон не достигает энергии фотоионизации, то мы имеем дело с физическим процессом, который является эффектом нагревания. Энергия поглощенного фотона будет обнаруживаться как кинетическая энергия молекулы.
Если резонансный фотон соответствует частоте фотоэффекта, то наблюдается химический процесс, так как из электрохимии известно, что процессы потери или приобретения электронов являются химическими реакциями. Энергия поглощенного фотона будет обнаруживаться как потенциальная энергия молекулы».
Здесь следует сделать уточнение: увеличение кинетической энергии молекул за счет внешнего излучения может иметь также и резонансный характер (например, при облучении вещества сверх высокочастотным (СВЧ) электромагнитным полем). СВЧ генераторы используются в качестве нагревательных устройств, в которых материал, подлежащий термообработке, нагревается за счет поглощения энергии электромагнитного излучения. Такие генераторы применяют для плавки металлов, нагрева материалов и даже в быту – для приготовления пищи.
Первое, что удалось установить, что при воздействии СВЧ излучения на различные вещества они нагреваются с различной интенсивностью. И даже может случиться так, что некоторые вещества вовсе не будут нагреваться. Все зависит от частоты излучения. Чем ближе она к собственной частоте колебания атомов (молекул) вещества, тем интенсивнее ими поглощение энергии излучения. Электромагнитное поле выступает здесь как внешняя «раскачивающая» сила, которая может войти в резонанс с собственным колебательным движением атомов (молекул).
Атом представляет некоторую пространственную конструкцию, сотоящую из элементарных частиц, имеющих массу и определенным образом взаимодействующих между собой. Эта конструкция обладает собственной частотой колебания, которую не сложно расчитать (учитывая наш вывод, что электроны не вращаются, в классическом понимании, вокруг ядра, а двигаются прямолинейно). Воздействуя на атомы внешними силами с частотой колебания, близкой к их собственной частоте, можно добиться резонанса, при котором нелинейно возрастает амплитуда колебаний (теоретически до бесконечности).
Резонансный характер увеличения кинетической энергии может быть подтвержден экспериментально. Оказалось, что частота СВЧ генератора, используемого в бытовых микроволновых печах, совпадает с собственной частотой атомов кислорода. Кислород, как известно самый распространенный химический элемент на земле. В виде химических соединений он составляет половину массы земной коры, входит в состав всех органических соединений, чем и объясняется широкое использование микроволновых печей в быту. Собственная частота атомов кислорода как раз и находится в пределах частоты СВЧ излучений (3*108 -3*1011 Гц). И именно атомы кислорода возбуждаются электромагнитным излучением в микроволновых печах. Это легко продемонстрировать. Достаточно поместить в печь вещество не содержащее кислород и убедиться, что оно не нагревается.
Возьмем к примеру парафин. Он, как известно, представляет собой смесь насыщенных углеводородов состава C18H38 - C35H72.
Температура плавления парафина всего 40 - 65оС. Но если его поместить в микроволновую печь, то он не плавится. Получается очень эффектный опыт с обычной парафиновой свечой (у свечи необходимо отрезать фитиль, иначе он может загореться и печь выйдет из строя). Ни в коем случае нельзя брать цветную свечу, поскольку краситель, как правило, органического происхождения и содержит кислород - свеча расплавится. Обычная же белая парафиновая свеча остается холодной. Основание ее конечно немного размягчится от нагрева стеклянной подставки в камере печи. Кроме того, частично повысится температура воздуха в камере печи, от чего свеча так же нагреется, но ни в коем случае не расплавится. Интересен сам опыт со свечой. При нагреве в микроволновой печи фитиль свечи превратится в золу, поскольку содержит органику, а значит и кислород. Вместе с фитилем из сердцевины свечи выплавится немного парафина и в свече появится сквозное вертикальное отверстие вместо фитиля, но сама свеча не потеряет форму и останется холодной.
Таким образом, можно утверждать, что электромагнитным полем можно избирательно управлять кинетической энергией молекул конкретного вещества. А в случае химической реакции - говорить об управлении самой реакцией, если она зависит от температуры реагента. При этом СВЧ излучение будет выполнять функцию катализатора.
Если рассматривать реакцию горения, то при катализе кислорода СВЧ излучением за счет его активации будет происходить более полное сгорание топлива и увеличение скорости реакции. А это значит, что при тех же условиях рассеивания выделяемой энергии температура в плазме факела будет больше температуры при неактивированной реакции.
Мы не будем в этой статье подробно останавливаться на всех полученных в экспериментах результатах. Отметим только, что резонансный характер увеличения кинетической энергии реагентов при их облучении, приводящий к возможности управлять физико-химическими реакциями может быть широко использован в различных областях, и в первую очередь там, где требуются высокие температуры и скорости этих реакций.
Например, это может найти применение в двигателях внутреннего сгорания. Одна из основных характеристик двигателей – их экономичность, что во многом зависит от полноты сгорания топлива и температуры его горения. Попытка активации топлива, воздействуя на него электромагнитным полем, уже предпринималась для карбюраторных двигателей легковых автомобилей. В продаже можно встретить устройство – «Ионизатор топлива», применение которого предполагает экономию бензина. Не будем анализировать эффективность этого устройства, отметим только, что частота электромагнитного поля, создаваемого устройством равна частоте тока катушки зажигания, что на несколько порядков ниже частоты СВЧ излучения, а значит не приближается к собственной частоте колебаний молекул топлива. Кроме того, для более полного сгорания топлива необходимо активировать не само топливо, а окислитель – кислород воздуха, подаваемого в карбюратор.
Вторая (возможная) область применения катализа СВЧ излучением – процессы, где требуется подавление скорости реакций, если один из реагентов специально вводится в реактор для снижения ее скорости. Если частота излучения будет соответствовать резонансной частоте молекул реагентов, препятствующих реакции (например, горению), то возможно говорить о разработке методов и технических устройств подавления очагов возгорания.
Автор благодарит известного аналитика В.М.Капустяна за ценные советы и замечания, высказанные при обсуждении статьи.
1. Математический энциклопедический словарь.- М.: Сов. Энциклопедия, 1988.-847 с.
2. А.С.Компанеец, Принцип неопределенности. – М. : Знание, 1966. – 48 с.
3. Е.А.Трофимов, К вопросу об аксиоматике геометрии, -М.: Объединенный научный журнал № 10(33), Изд. «Тезаурус», 2002.-с 38-40.
4. Луи де Бройль, Революция в физике (Новая физика и кванты), 2-е издание, Перевод с французского, -М.: Атомиздат ,1965. - 232 с.
5. П.Г.Кузнецов, Фотоника, Приложение в кн.: Ю.В.Громыко, Метапредмет проблема, -М. 1998. –376 с.